Un exemple simple d'un filtre de fréquences.
Nous allons illustrer l'utilisation de filtres de fréquences dans le cas simple et souvent rencontré où le bruit est bien plus large-bande que le signal. Nous proposons un signal avec une formule un peu compliqué:
s(t) = cos(3.02*t).*sin(20.81*sin(t)+2*t)
On peut s'imaginer la valeur de la fonction donnant le signal en mV, et le temps t en secondes (mais on pourrait considérer la variante où ce sont des millisecondes ou des microsecondes). Dans le reste de cet exemple, nous considérons que t soit en secondes. Le signal est donc très basse-fréquence et on pourrait imaginer qu'il provienne d'un capteur mécanique qui décrit une ou autre mouvement. L'expression du signal ci-dessus génère une certaine richesse spectrale. Un petit morceau du signal a l'aspect suivant:
La densité spectrale de ce signal (en unités arbitraires car en réalité il contient des pics de Dirac) prend la forme suivante:
Nous observons que le contenu spectrale du signal se situe entre 0 Hz et 5 Hz, où les plus grandes fréquences ont de faibles amplitudes. C'est la seule information que nous allons utiliser de notre signal: le fait que son spectre de fréquences se situe entre 0 et 5 Hz. Ainsi, le filtre adapté à cette information est un filtre de fréquences.
Si maintenant nous ajoutons du bruit au signal, pour simuler le signal bruité dont nous disposons. Le bruit est 'blanc' avec une valeur RMS de 1 mV. En réalité la bande du bruit est entre 0 et 50 Hz. Le signal aura alors l'aspect suivant:
Clairement à l'oeil, on ne peut plus distinguer le signal original. Le spectre de ce signal bruité est:
Nous voyons que le spectre du signal sort du spectre du bruit blanc. Il suffit donc de sélectionner du signal que la partie utile. Il y aura de toute façon une contamination du bruit, car il y a du bruit présent dans la bande utile du signal: ce bruit-là ne pourra pas être enlevé par un filtre de fréquences. Nous voyons aussi que bien que nous savons que le signal a des composantes jusqu'à 5 Hz, en fait au-delà de 4 Hz, ces composants sont plus faibles que le bruit: il ne sert donc à rien de vouloir garder la bande entre 4 Hz et 5 Hz, car il y a plus de bruit que de signal dedans. Ainsi, il nous paraît bien d'avoir un filtre qui laisse passer la bande 0 - 4 Hz, et qui coupe tout le reste. Si nous appliquons ce filtre parfait au signal bruité, nous obtenons:
Bien que le signal en sortie de ce filtre (bleu) n'est pas identique au signal d'origine (vert), ceci est attendu: il y avait du bruit dans la bande utile que nous ne pouvions pas enlever. Cela dit, le signal filtré ressemble beaucoup plus au signal d'origine que le signal bruité. C'est le mieux qu'on puisse faire si nous nous limitons à l'information de la bande utile de fréquences du signal. Pour faire mieux, il faudrait utiliser d'avantage d'informations du signal et éventuellement, du bruit.
Maintenant, nous pouvons nous poser la question: la déviation entre l'original et le signal filtré peut avoir deux causes: le bruit que est passé dans le signal de sortie, et le fait que le filtre ait modifié le signal même (car nous avons coupé à 4 Hz, et le signal contient de l'énergie jusqu`à 5 Hz). Quel est l'effet du filtre sur le signal d'origine même ?
Nous voyons que le signal filtré a quelques oscillations supplémentaires (enre 70.5 et 71 secondes, et entre 73.5 et 74 secondes par exemple). Mais ce sont de petites déviations comparé aux déviations due au bruit dans l'illustration précédente. C'est donc bien le bruit que domine la déviation entre le signal filtré et l'original. Cela justifie le fait de couper à 4 Hz et non à 5 Hz: nous coupons ainsi 1/5 du bruit qui restera dans le signal filtré.
On pourrait se demander pourquoi s'embrouiller avec des filtres approximatifs, si le filtre parfait est possible (comme nous avons fait pour produire les illustrations). Le problème est que pour pouvoir appliquer le filtre parfait, il faut déjà avoir le signal en entier. Ensuite, il faut en faire la transformée de Fourier, limiter cette transformée à la bande passante (ici donc 0-4 Hz), et prendre la transformée inverse: ce sera le résultat du filtre parfait appliqué au signal. C'est ce que nous avons fait pour calculer la sortie du filtre parfait.
Un vrai filtre doit traiter le signal pendant qu'il arrive dans la plupart des cas. Il ne peut pas attendre la fin du signal pour commencer à produire le signal de sortie. Nous avons implémenté une simulation de 3 filtres classiques: un filtre Butterworth coupant à 4 Hz, un filtre Tchebychev de type I coupant à 4 Hz avec une erreur permise de 10% dans la bande passante, un filtre Cauer coupant à 4 Hz, aussi avec une erreur d'amplitude permise de 10% dans la bande passante, et une suppression d'au moins 100 dans la bande supprimée. Nous nous limitons à des filtres d'ordre 3.
Le résultat de l'application de ces filtres au signal bruité est comparé au signal d'origine, et au résultat du filtre parfait:
La première chose qui frappe, c'est que la sortie des filtres réels ont un retard comparé au signal d'origine, ou du filtre parfait. Effectivement, des filtres réels, et donc respectant la causalité, doivent opérer avec un délai. Ici, ce délai s'avère être de l'ordre de 0.2 secondes. En suite, nous constatons que les 3 filtres ont des réponses très similaires. Le filtre Butterworth dévie le plus, mais comme cette déviation est petite comparée à la déviation du filtre parfait du vrai signal, nous ne pouvons pas dire que le filtre Butterworth a une performance moindre que les deux autres.
Le filtrage en amplitude théorique de ces 3 filtres est:
Les propriétés classiques sont reconnues: le filtre Butterworth a la plus lente coupure, mais a la réponse la plus plate dans les basses fréquences. Le filtre Tchebychev de type I a son oscillation permise de 10% dans la bande passante, mais a une coupure bien plus franche. Le filtre Cauer (elliptique) est encore plus raide, mais le filtre Cauer remonte dans la bande coupée, tandis que le filtre Tchebychev continue de descendre.
Le cas illustré est très simple, mais on le retrouve souvent: nous avons un signal utile dont nous savons qu'il est limité à une bande passante bien plus étroite que le bruit qui est large-bande. Si c'est la seule information que nous avons, ou que nous voulons utiliser, le filtre le mieux adapté au problème est un filtre de fréquences qui limite la bande passante à celle du signal utile. Dans notre exemple, ce filtre ne doit pas être très sophistiqué. Nous ne voyons presque pas de différences en qualité entre le filtre parfait, et des filtres classiques de troisième ordre. Il n'y a pas lieu de faire des choses compliqués et cependant, le résultat est impressionnant: d'un signal bruité dans lequel nous ne pouvions pas reconnaître la forme du signal utile sort une reconstruction, bien qu'elle n'est pas parfaite, contient beaucoup d'aspects du signal original.
Implémentation
On peut se demander si nous allons réaliser ce filtre dans le domaine analogique ou numérique. Le premier réflex serait de le faire de façon numérique. Effectivement, les fréquences sont très basses dans cet exemple (moins que 50 Hz). En plus, la dynamique du signal au-dessus du bruit est petite. Il nous faut donc seulement un convertisseur lent avec peu de dynamique. Même des contrôleurs ont souvent un ou quelques ADC de ce type intégrés. Seulement, pour pouvoir numériser, il faut de toute façon déjà un filtre passe bas anti-repliement. On peut se demander quel peut être le gain de fabriquer un filtre anti-repliement qui coupe à 20 KHz avec un ADC qui échantillonne à 40 Ké/s pour implémenter un filtre numérique à 4 Hz. Nous allons voir que la question n'est pas aussi vite tranchée et la proposition n'est pas aussi ridicule qu'elle peut en avoir l'air. Il se peut qu'un filtre anti-repliement (forcément analogique) à 20 KHz est bien plus commode à construire qu'un filtre à 4 Hz. Si les deux filtres sont de complexité, qualité, commodité et prix, comparable, ce n'est que dans ce cas que le choix est évident et qu'il n'y a aucune raison de le faire de façon numérique. Le fait que le filtre peut être relativement simple pour résoudre le problème donne un avantage potentiel à l'analogique.
Si nous choisissons le filtre analogique, il faut encore décider: passif ou actif ?
La synthèse d'un filtre en forme passive peut conduire à un circuit comme celui-ci:
Le filtre Cauer:
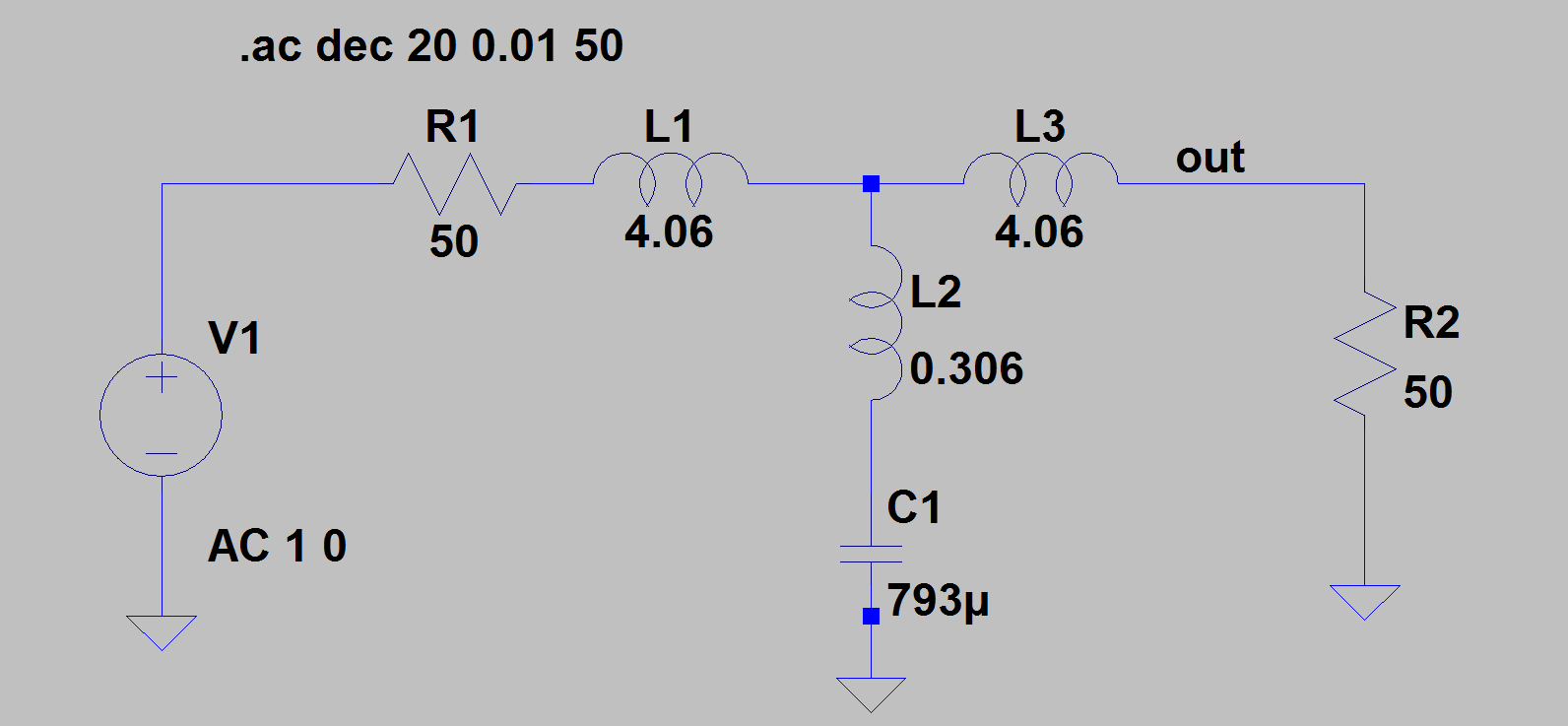
et le filtre Butterworth:
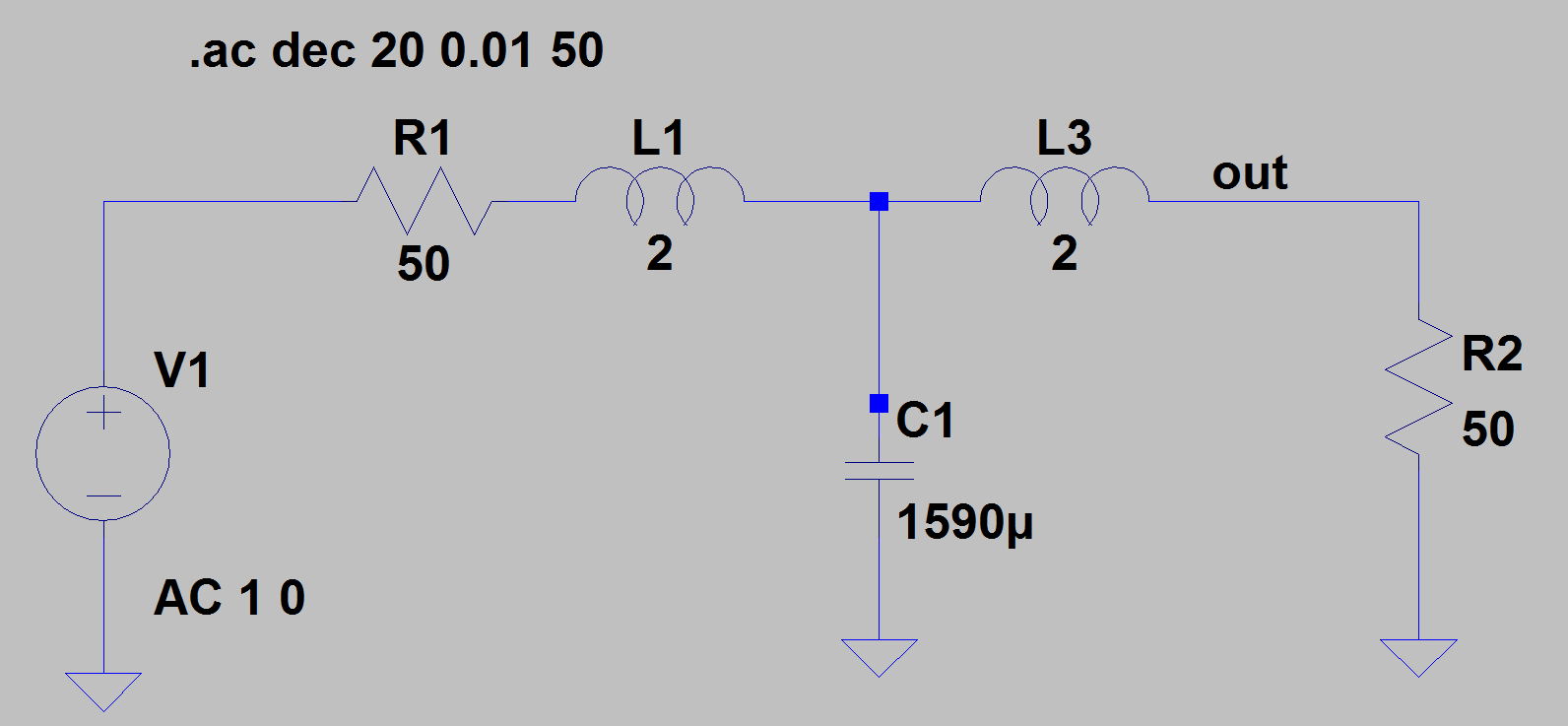
Nous constatons que les valeurs ne sont pas pratiques du tout: des Henry's et des milli-farad. Ces larges valeurs pour les inductances et les condensateurs se traduiront par des composants chers, gros et loin d'être idéal. C'est toujours le cas pour des filtres passifs à basse fréquences. Si nous avions considéré que l'unité de temps est la micro seconde au lieu de la seconde, alors il faudrait un filtre qui coupe à 4 MHz. Le même filtre aurait des inductances dans les quelques micro-Henry, et les condensateurs seraient au tour de 1 nF. Ce filtre aurait des composants petits, pas chers et compacts, qui sont assez bon marché.
Si nous voulons considérer un filtre actif, la réalisation du filtre Tchebychev I peut prendre la forme suivante:
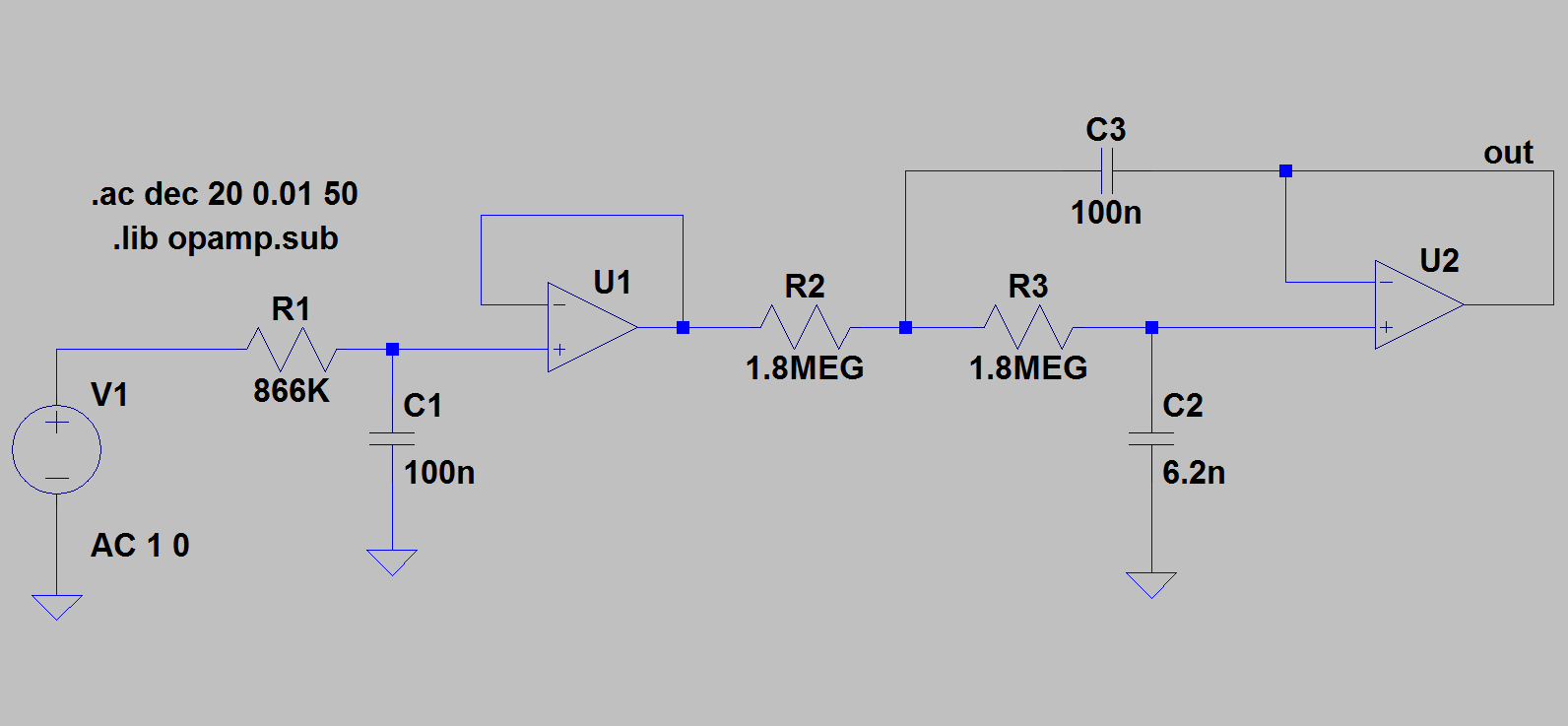
Le filtre actif se réalise donc avec des composants bien plus commodes.
Même un filtre Cauer peut être réalisé avec une augmentation modeste du nombre des composants:
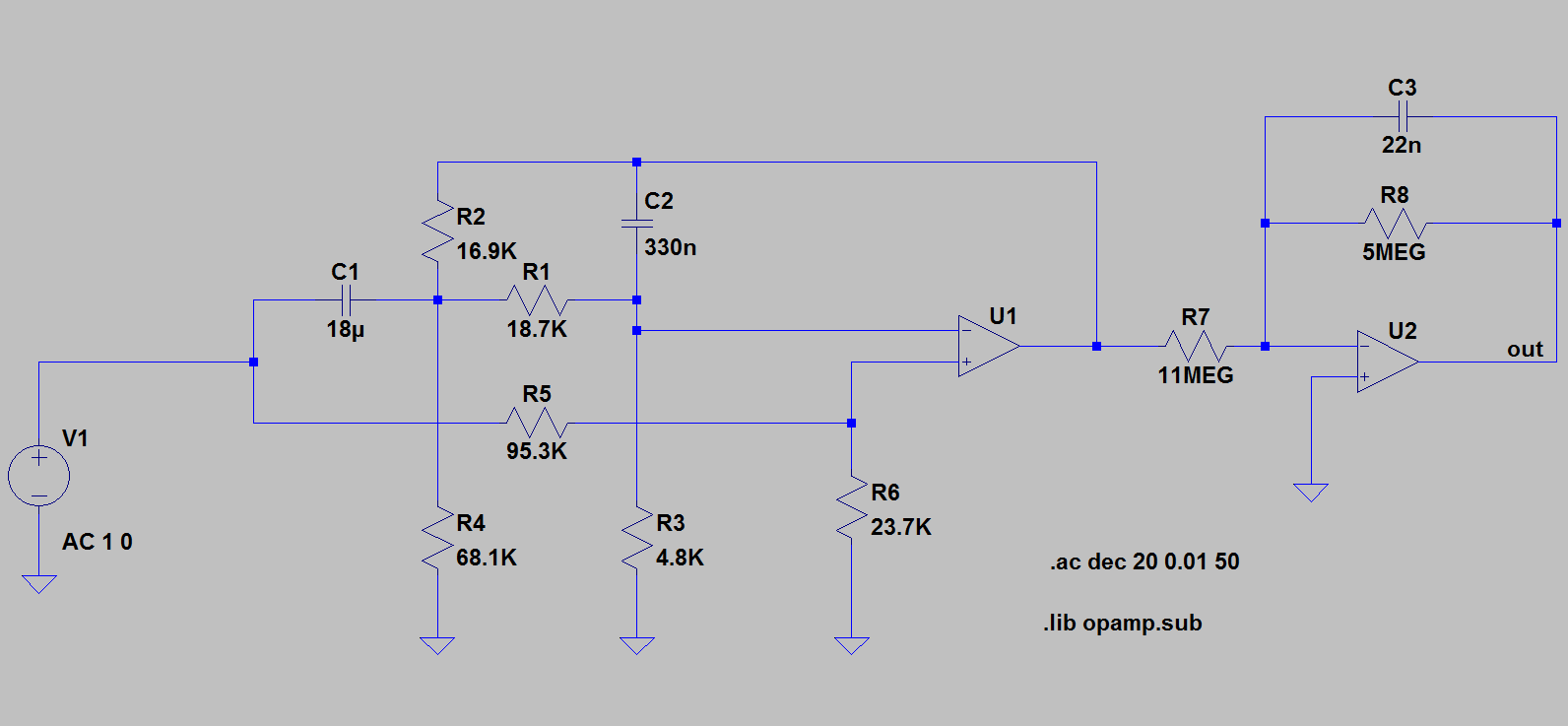
Considérons maintenant la variante numérique. Comme nous avons évoqué précédemment, il nous faudra de toute façon un filtre anti-repliement. Il peut donc sembler inutile, à première vue, d'utiliser un filtre numérique, car il nous faut de toute façon ce filtre analogique. Seulement, dans ce cas précis, étant donné la très basse fréquence nécessaire, nous pouvons satisfaire le besoin d'un filtre anti-repliement avec un filtre très simple. Considérons une coupure pour le filtre anti-repliement à 4 Hz. Un filtre de première ordre coupera à 20 dB par décade. A 4 KHz, nous avons donc déjà une coupure de 60 dB. Pour atteindre 40 dB de suppression (notre exigence pour le filtre Cauer), 400 Hz sont suffisantes. Un taux d'échantillonnage à 8 Ké/s est donc largement suffisant. Mais 10 Ké/s sont une trivialité pour beaucoup de convertisseurs et le filtre anti-repliement se limite donc à un simple filtre RC. Le filtre numérique coupera alors plus précisément à 4 Hz.
Si nous utilisons un contrôleur, et un taux d'échantillonnage à 10 Ké/s, le rapport entre le taux d'échantillonnage et la bande passante est de 2500. C'est l'ordre de grandeur du nombre de taps qu'un filtre FIR aura besoin (c'est la taille mesuré en échantillons de la réponse impulsion) Disons que notre filtre FIR nécessite 10 000 taps. Cela veut donc dire, 10 000 multiplications et 10 000 additions par échantillon de sortie, ou 200 millions d'opérations flottantes par seconde. Pour un simple contrôleur, ce sera un peu stressant ! Bien sûr, ces taux peuvent facilement être atteint par un FPGA ou un DSP, mais cela fera un système bien plus cher.
En réalité, quand le rapport entre la fréquence d'échantillonnage et la bande passante du filtre est très grand, il faut opter pour un filtre IIR dans la mesure du possible. Le filtre IIR sera la version numérique du filtre analogique standard. Nous allons simplement considérer la construction IIR dans cet exemple. Le filtre Butterworth de 4ième ordre prendra la forme suivante (dans un langage indéfini), il faudra exécuter ce code pour chaque échantillon:
a1 = 0.9998;
a2 = 3.9992;
a3 = 5.9988;
a4 = 3.9992;
a5 = 0.9998;
b1 = 0.9934540;
b2 = - 0.9803406;
b3 = 5.98039191;
b4 = - 3.9934325;
scale = 2.486e-12;
in(5) = in(4);
in(4) = in(3);
in(3) = in(2);
in(2) = in(1);
in(1) = newin;
outnew = a1 * in(5) + a2 * in(4) + a3 * in(3) + a4 * in(2) + a5 * in(1);
outnew = outnew - b1 * out(4) - b2 * out(3) - b3 * out(2) - b4 * out(1);
outnew = scale * outnew;
out(4) = out(3);
out(3) = out(2);
out(2) = out(1);
out(1) = outnew;
Nous pouvons aussi construire le filtre elliptique avec le même code: seulement les valeurs des constantes change!
a1 = 0.0099881;
a2 = -0.0399512;
a3 = 0.0599264;
a4 = a2;
a5 = a1;
b1 = 0.9975666;
b2 = -3.99269;
b3 = 5.9926803;
b4 = -3.9975568;
scale = 1.0;
Contrairement à la réalisation analogique, la version numérique d'un filtre Cauer n'est pas plus compliquée que celle d'un filtre pure pole. La raison est que le filtre Tchebychev ou Butterworth n'est plus "pure pole" dans le domaine numérique: ils ont des zéros finis comme le filtre Cauer. S'il y avait une raison d'économie de composants ou de simplicité de réalisation dans le domaine analogique qui nous fait préférer les filtres pure pole, cela ne change rien pour le domaine numérique. C'est l'origine d'un intérêt plus prononcé pour les filtres Cauer dans le domaine numérique.
Les deux filtres nécessitent une vingtaine d'opérations flottantes (10 additions et 10 multiplications environ). C'est donc 200 000 opérations flottantes part seconde, ce qui est largement dans les spécifications de la plupart des contrôleurs. Bien sûr il est parfaitement possible de réaliser le filtre numérique avec un petit FPGA, qui peut s'acheter pour quelques dizaines d'euros (sans compter l'ADC).
Conclusion
Nous avons illustré un cas fréquent d'utilisation de filtre de fréquences: limiter la bande passante d'un signal contaminé avec du bruit, par la portion utilisé utilement du spectre par le signal. Cela marche surtout bien quand le bruit est très large bande et le signal a une bande bien plus petite. Nous avons construit un exemple artificiel avec un signal très basse fréquence (comme on en trouve avec des capteurs mécaniques par exemple). Dans cet exemple, un filtre actif analogique ou un filtre numérique est à priori le meilleur choix. Nous avons constaté que le filtre peut être relativement simple pour éliminer le bruit large bande. Le filtre Elliptique est plus compliqué que le filtre Butterworth ou Tchebychef I dans le domaine analogique, mais c'est parfaitement la même complexité dans le domaine numérique.
Cet exemple ne montre pas la pertinence d'un filtre plus puissant.

