The circuit
We consider a very elementary Common Emitter amplifier with a general purpose transistor: the BC547B.
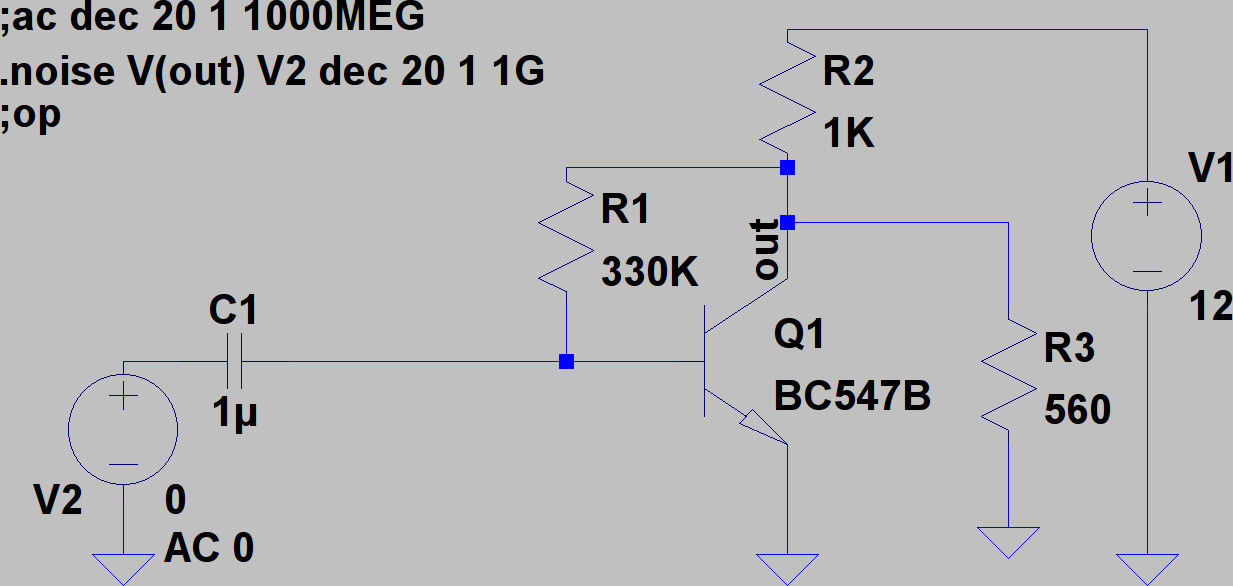
To the left, there is the signal source that is to be amplified, and R3 is the load resistor.
We use LTSpice to calculate the operating point of the circuit and we find:
V(out): 3.42558 voltage
V(n003): 0.662143 voltage
V(n001): 12 voltage
V(n002): 0 voltage
Ic(Q1): 0.00244894 device_current
Ib(Q1): 8.37405e-006 device_current
Ie(Q1): -0.00245732 device_current
I(C1): 6.62143e-019 device_current
I(R3): 0.0061171 device_current
I(R2): 0.00857442 device_current
I(R1): 8.37405e-006 device_current
I(V2): 6.62143e-019 device_current
I(V1): -0.00857442 device_current
Analytical noise estimation
As we said before, one needs to perform an analytical noise estimation to verify whether the SPICE model that will be used further on, has a good noise description of the components. For discrete components, the noise model is built into SPICE, so that should in principle be OK. For models of integrated circuits that is less evident. So we expect here that SPICE will give us the correct results. Nevertheless, we will illustrate a calculation.
We will use a very simple transistor model: the Ebers-Moll model in its simplest form. The transistor itself has two fundamental noise sources: the shot noise of the basis-emitter current, and the shot noise of the collector-emitter current.
For the shot noise of the collector-emitter current, we can make the following small signal AC model:
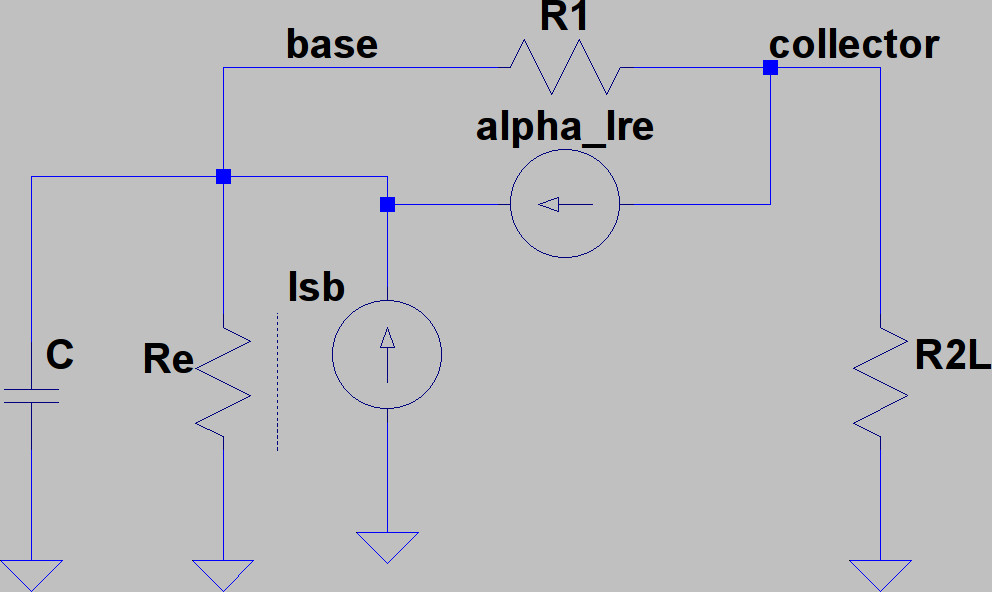
We R2L is the parallel of R2 and R3 (or the load resistor) and is 360 Ohm. Re is the dynamic base-emitter resistance, which is VT / IE with VT = kB T/q = 26 mV.
Given the calculated emitter current of 2.46 mA, Re = 10.6 Ohm
Alpha in the dynamic current source can be calculated from the transistor beta, which we take to be the ratio of the collector current over the base current. From the calculation above, we obtain:
beta = 2.45 mA / 8.37 μA = 293
alpha is hence 1 - 1/beta.
It is true that we commit an error here by confusing the large signal gain and the small signal gain, but for our estimation, this will be good enough. The shot noise source Isb is introduced between the emitter (which is at ground) and the base). It will have a white spectrum with density:
Ssb(f) = 2 q IB = 2.68 10-24 A2/Hz
We can now solve the linear circuit, and I used the node voltage method, with two nodes: node 1 is the base, and node 2 is the collector. The analytic equations can be put into an (open source) program like wxMaxima, and what we are after is the transfer function from the source Isb to the output voltage, which is equal to v2 in our case.
![]()
Putting in the numbers, we find that the output voltage is given by:
v2 = - isb { 1.08 108 / (3.18 s + 1385) Ohm }
The transfer function is hence a single pole transfer function. Its low frequency value is 7.8 104.
The pole resides at 1385 / (2 π 3.18) Hz = 69 Hz.
The noise spectral density contribution to the v2 from the base shot noise at low frequencies will then be
S1(f = 0) = (7.8 104)2 2.68 10-24 V2/Hz = 1.63 10-14 V2/Hz = (128 nV)2/Hz
This noise contribution will start to fall at 20 dB/decade from 69 Hz onward.
We now do the same kind of calculation for the collector shot noise:
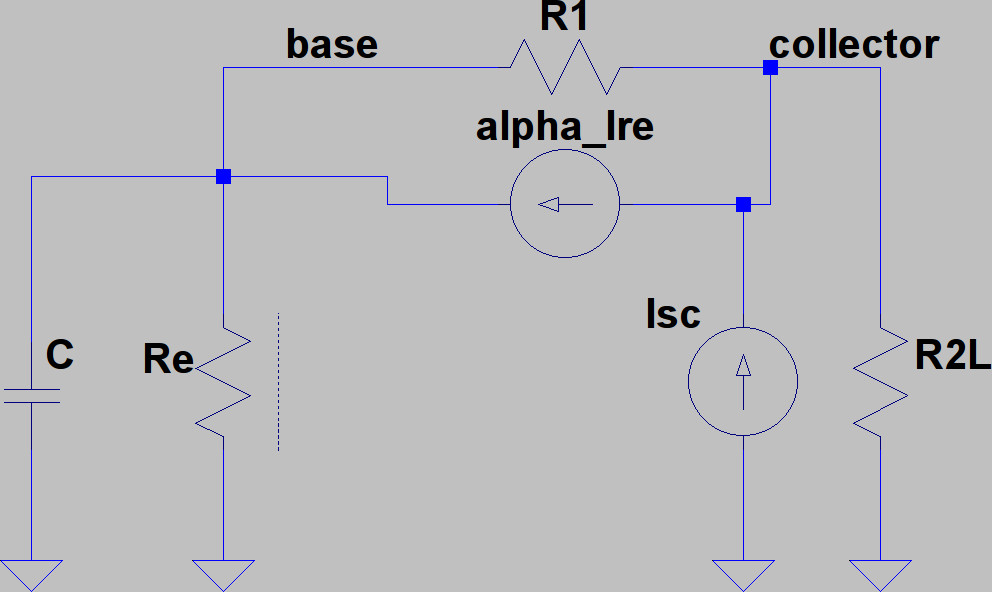
The small signal circuit is of course the same as the previous one, but we now have the collector-emitter shot noise source Isc between the emitter (at ground potential) and the collector.
The spectral density of this current noise source is:
Ssc(f) = 2 q IC = 7.85 10-22 A2/Hz
A similar analytical calculation with MxMaxima results in the following expression for the output voltage:
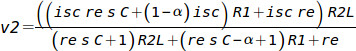
Filling in the numbers, we find that:
v2 = isc { (1145 s +1035) / (3.18 s + 1385) } Ohm
We see that the transfer function has a single pole and a single zero. The pole is at 69 Hz (it is the same pole as for the base shot noise transfer function), while the zero is at 0.14 Hz.
The (very) low frequency limit (far below 0.14 Hz) of the transfer function is: 1035/1385 = 0.75 Ohm.
The high frequency limit (far above 69 Hz) of the transfer function is 1145/3.18 = 360 Ohm (note that this is essentially the load resistor).
In the high frequency limit, the contribution to the voltage noise spectral density at the output will be:
S2(f >> 69 Hz) = (360)2 7.85 10-22 = 1.02 10-16 V2/ Hz = (10.1 nV)2 / Hz
As below 69 Hz, the transfer function lowers, the spectral density contribution will be lower than this. Now, we know that the contribution from the base shot noise is already (128 nV) squared per Hz, so this will be invisible.
Conclusion of the calculation:
We expect the noise spectral density for frequencies below 69 Hz to be about (128 nV)2 / Hz, dominated by the base shot noise. Then we expect the spectral density to fall, at 20 dB per decade, to the value of about (10.1 nV)2 / Hz and remain constant there (until our model is not valid any more and high frequency effects which we didn't take into account, start to take effect.
Note that we didn't complete the calculation. Normally we should also have done the calculation for the thermal noises of the resistors R1 and R2L. It will turn out that their contributions are negligible - but that is something one can only find out when doing the calculation of course...
Spice simulation of the noise
When performing the SPICE noise spectral density calculation using LTSpice, we obtain:
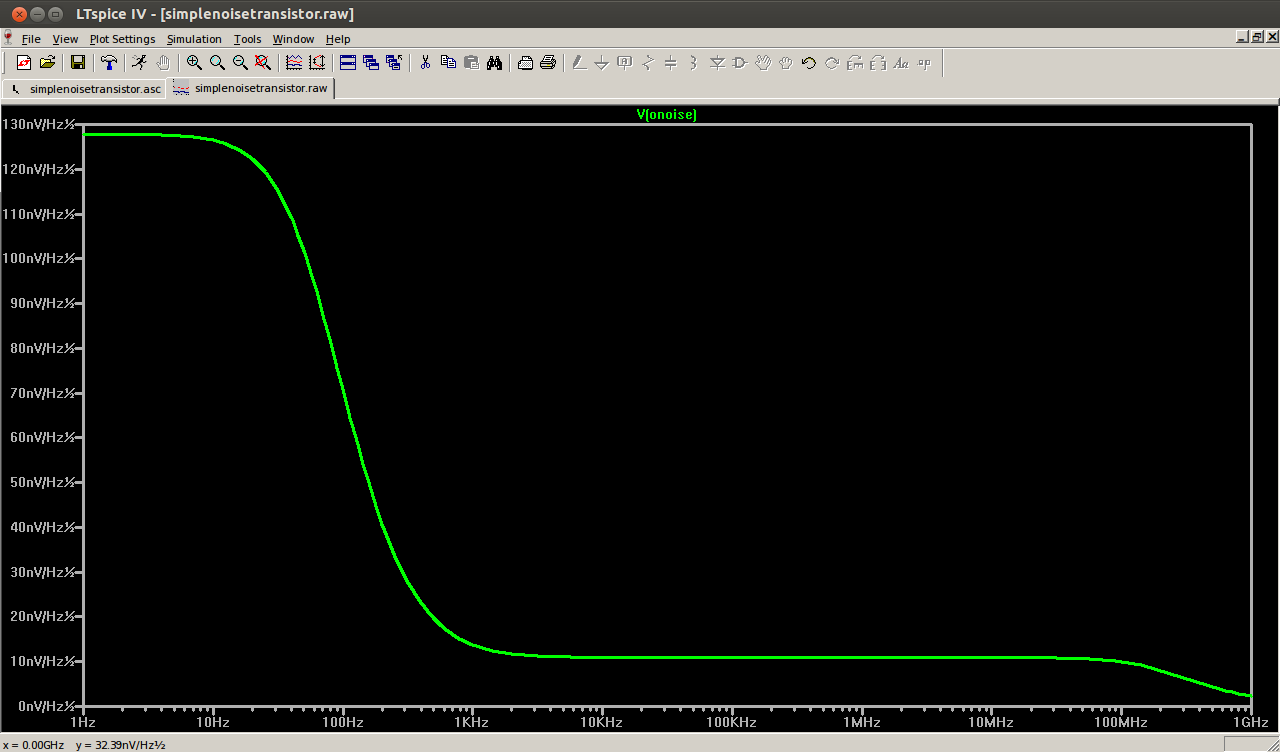
Note that the quantity that is displayed is the square root of S(f), in units of V per square root Hz.
We see that our analytical estimation is in agreement with the SPICE calculation: to the left, we are not very far from our 128 nV per square root Hz, and in the middle, we are around 10 nV per square root Hz.
The SPICE simulation allows us to integrate the noise spectral density, which gives us the RMS voltage noise on the output: it turns out to be 184 μV. This is a pretty high value. Any time sample of the output voltage has (presumed Gaussian) error on it due to the noise, with a standard deviation of 184 micro volt.
Noise referred to the input
If we are only interested in the mid-band behaviour and we want to reduce the output noise back to the input signal, it turns out that the equivalent input noise spectral density is (0.35 nV)2 / Hz (where the output noise spectral density is (10.9 nV)2 / Hz ). The integral gives us an equivalent input RMS value of 11.9 μV.
We might think that, because the dominating contribution is the collector shot noise which has a spectral density, proportional to the collector current, that choosing a bias point of the transistor with a smaller collector current will reduce the output noise.
We can easily test this by changing R1 from 330K to 1600K and by changing R2 from 1K to 5K. We keep the load of course to 560 Ohm, as this is supposed to be an external given ("drive a 560 Ohm load"). The collector current is now diminished from 2.44 mA to 0.10 mA. The base current went down from 8.37 μA down to 0.36 μA. With these parameters, a SPICE noise calculation gives us a noise spectral density at the output of (4.1 nV)2 / Hz, which is indeed more than twice below the output noise level we had with the higher bias currents. However, the gain of the amplifier has diminished too, and now, the equivalent input noise spectral density is (2.06 nV)2 / Hz instead of (0.35 nV)2 / Hz, with an integral which gives an equivalent input RMS value of 35.4 μV, so we see that with a smaller bias current, the input is actually more polluted than with a higher bias current even though the output is less noisy.
If the amplifier is supposed to treat information that was present in the input voltage signal, and if we assume that the useful signal bandwidth corresponds more or less to the passband of the amplifier, which according to a SPICE calculation is about 200 MHz, then, if the input signal has an RMS value of 10 mV, we can use Shannon's information theorem to say that the original amplifier can transmit about 2 Gb/s of information of the original signal. With the low-bias current variant, this will be 1.6 Gb/s.
Conclusion
The analytical estimation, on the basis of a very simple model of the device, showed us that the SPICE calculation did take into account at least the fundamental noise sources of shot noise in the base and the collector. The analytical calculation also indicates what noise sources are dominant, and where: the base shot noise is dominant at low frequencies, the collector shot noise is dominant in the mid band of the amplifier. They are the two dominant noise sources, and the resistor thermal noise has no significant contribution.
Moreover, the fact that it are fundamental noise sources means that with the same biasing, the noise of the circuit is not dependent on the particular transistor technology: any other transistor with the same biasing will yield (at least) the same noise. Given that in the mid band, it is the collector noise that is dominant, means that even a transistor with a higher beta will not improve much on the situation.
If we would have build the circuit, we would also have been able to compare these results to measurement. It is not possible to have lower noise than what has been calculated, because the calculated noise comes from unavoidable, fundamental sources. If the measured noise is higher, this indicates that there are technological noise sources that have not been taken into account by the SPICE model, or that there are other problems with the circuit (such as pick up noise).

